レーティングシステムの説明

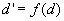
　作家の人気は、なによりも売上で示されねばならない。
　とはいえ、児童文学とトラベルミステリーの比較はあまり意味がない。前提条件があまりにも違っているからだ。ある程度共通の条件のある場合にしか、「売上≒人気」は成り立たない。
　幸い、ボーイズラブは均質性が高い。販路、装丁、読者層、いずれも高い均質性を示している。このような環境で「売上≒人気」が成り立たないとしたら、人気という概念は意味を持たないだろう。
　もし売上数のデータが手に入るなら、そこから単純に人気を割り出すことができる。あいにく、そのような情報は公開されていないため、週間ベストセラーリスト（トーハン・日販調べ）の分析によって人気を推定することを試みた。
　週間ベストセラーリストに含まれる情報は、売上数より扱いにくい。第一に、どの本がどの本より売れたか、という情報しか得られない。第二に、発売日の異なる本のあいだでは比較が成り立たない。つまり、同一レーベル間の順位しか意味を持たない。このため、「どの本がどの本より売れたか」という情報も、きわめて限られたものになる。
　このような限られた情報から人気を推定するために、本研究では、チェスなどで用いられている「レーティング」というシステムを拡張して用いた。レーティングシステムの基本的な性質を以下に示す。

プレイヤーのそれぞれが持ち点を与えられ、勝敗によって増減する

　勝てば持ち点が増え、負ければ減る。

全プレイヤーの持ち点の総和が不変

　持ち点の増減は、原則的に、プレイヤー間の持ち点の移動から生じる。よって、点数の絶対値には意味はなく、プレイヤー間の点差だけが意味を持つ。

順当な結果では持ち点の移動が少なく、番狂わせでは大きい

　つまり、金星と白星の重みが違う。ザコを何匹倒しても、大物を仕留めたプレイヤーには敵わない。

勝負の重み付けの方法

　金星と白星の重みが違うといっても、点数としては具体的にどうなるのか。このシステムでは点差だけが意味を持つので、これは次式で表現される。

ただしdは対戦前の（勝者の持ち点 - 敗者の持ち点）、d'は対戦後の（勝者の持ち点 - 敗者の持ち点）とする。
　チェスでは現在は関数fに一次関数を用いているが、これはあまりにも点差の開いている相手とは対戦しないとの前提にもとづいている。このため、本研究では、関数fを独自に定義した。
　作家の人気にいつまでも変化が生じない世界を想定し、これを「理想世界」と表記することにする。理想世界では、無限に多くの測定（週間ベストセラーリスト発表）が行えるので、人気を一意に反映する「人気度」という値を想定することができる。理想世界においては、持ち点＝人気度であるとし、理想世界のdをDと表記する。
　D > 0のとき、その対戦は順当な結果が出たことになる。Dが大きければ大きいほど、結果の順当さは増す。逆にD < 0なら番狂わせで、Dが小さいほど大番狂わせだ。D = 0なら勝負は五分五分である。
　このような勝率を表すものとして、関数rを考える。r(D)が確率を表す。
　関数rは次のような性質を備える。

　さらに、r(1) = 2/3と定義する。
　理想世界における3人のプレイヤーx, y, zを考える。持ち点はx > y > zとする。（xの持ち点 - yの持ち点）をD_xy、（yの持ち点 - zの持ち点）をD_yzとする。そして、D_xy = D_yz = 1とする。当然、D_xz = 2となる。では、r(2)はどんな値になるか？
　それは統計的データによってのみ決定できる、が答である。
　チェスのように豊富な統計的データがあれば、関数rは決定できる。しかし本研究では、そのようなデータは望むべくもない。このため、関数rを法外でない範囲で勝手に決めた。
　本研究では、関数rを次のように定義した。

　このように関数rを定義すると、将棋でいえば勝率10%が三段差（アマチュアの）になる。勝率1/10で三段差はない、せいぜい二段差と感じるが、いま問題になっているのはベストセラーリストであって将棋ではない。
　関数rが定義されたことで、Dの意味が決まった。次は関数fである。

　コインを投げて裏表のどちらが出るか、その確率を調べれば、たいていのコインでは表も裏も同じ0.5だろう。しかしここに、どういう仕掛けか知らないが、一方に偏って出るコインがあるとする。このコインを一度だけ投げたら、表が出た。では、このコインをもう一度投げたとき、表を出す確率はどんなものか、このたった一つの結果から推定せよ。
　小学生でも「100パーセント」とは答えないだろう。少なくとも0.5以上であることは確かだ。しかしなにをいうにも、たった一度の試行で「推定せよ」とはナンセンスではないか？
　ところが統計学というのは実に謎めいた学問なので、こういう問いにもちゃんと答えられる。正解は2/3である。
　なんの履歴もないプレイヤー同士が対戦したとしよう。このときの勝者が次の対戦でも勝つ確率は、もちろん2/3と推定される。
　とすると、持ち点の等しいプレイヤー同士が対戦したら（つまりd = 0）、d'はr(d') = 2/3になるように決める（つまりd' = 1）べきなのか？
　しかし、もしその「持ち点が等しい」というのが、過去100回の対戦を50勝50敗したあとのことだとしたら、どうか。過去の実績から見れば、2/3という値が無茶なのは一目瞭然だ。2/3という値は、履歴がない（あるいは無視する）、という条件での話で、履歴をみるなら、r(d')は2/3よりも小さな値でなければならない。もちろん、0.5を切るわけがないので、0.5 < r(d') < 2/3（つまり0 < d' < 1）となる。d'が小さいほど履歴の重みが大きいことになる。
　さて、レーティングシステムの「持ち点」という概念のなかには、履歴の重みの大小が含まれていない。初めてゲームに参加するプレイヤーも、100回の戦歴を持つプレイヤーも、履歴に対して同じ重みを与えなければならないわけだ。ちょっと理不尽なようだが、いずれにしろ履歴の重みを制限しないと、人気の変化に追随できなくなる。
　履歴の重みを表現する値として、f(0)を考えることができる。本研究では、f(0)=0.5と定めた。
　理想世界においては、対戦後の持ち点の期待値は、対戦前の持ち点と等しくなければならない。よって次式が成り立つ。