2012年01月01日
正規表現マッチングはMap-Reduceできる
グレゴリオ暦で新年を祝われる皆様、あけましておめでとうございます。
今日のお題は正規表現。ただしチューリング完全なPCREではなく、有限オートマトンにもとづく本来の正規表現である。
一個の巨大な文字列に対する正規表現マッチングをMap-Reduceで分散計算することはできないと思い込んでいるマヌケな子はいねーがー? できそうな気はするけれどアルゴリズムがわからないアホな子はいねーがー? 大丈夫、このエッセイを読むまで私にもわからなかった。アホはあなただけではない。といってもなんの慰めにもならないが。
(このエッセイは正規表現のインクリメンタルマッチングの計算量について論じているが、分散計算のほうが例として自然と思ったのでそうした)
英語とHaskellができてモノイドとfingertreeが常識な人なら元のエッセイを読めばすべて一目瞭然だと思うが、私は英語以外まるでダメなので、理解するまでにすさまじく時間がかかった。日本語でこの問題を説明しているサイトはどうもないようなので、ここに書き留めておく。なお正規表現と有限オートマトンは常識とする。
正規表現『.*(.*007.*).*.』に対応するステートマシン図は以下のとおり:
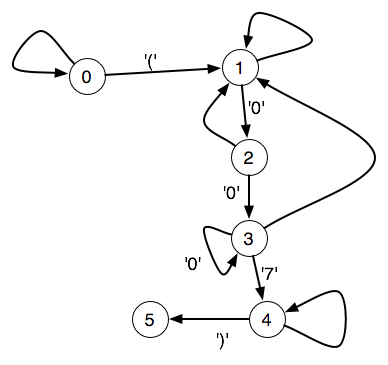
正規表現マッチングをごく手続き的に平凡に考えるなら、初期ステートの0にセットしたステートマシンを文字列の上に走らせ(テープの上を走るチューリングマシンのイメージだ)、完走後のステートを調べて、もし5ならマッチ、ということになるだろう。
このステートマシンは、自分自身のステート(0~5の6択)を文字ごとに逐次的に変更してゆくことで動作する。だから正規表現マッチングをMap-Reduceするにはどうすればいいかわからない、ということになる。
『abc(007007)abc』という文字列を例に、逐次的な変更の様子を見てみると:
state 0 0 0 0 1 2 3 4 4 4 4 5 5 5 5 string a b c ( 0 0 7 0 0 7 ) a b c
ステート0のステートマシンは走行開始直後にまず文字'a'を見て、自分自身のステートを0のままにする。'b'、'c'も同様にして通過し、文字'('を見てついに自分自身のステートを1に変更する。それに続く文字'0'を見てステートを2に――という具合だ。
上の表を見てわかるとおり、同じ文字'0'に対して、ステートマシンはさまざまな反応をしている。最初の文字'0'を見たときには、自分自身のステートを2に変更している。2度目の文字'0'を見たときには自分自身のステートを3に変更し、それ以降に見たときにはもう自分自身のステートを変更することはない。
もちろんステートマシンは文字'0'の出現回数を数えているわけではない。ステートマシンの動作(=自分自身のステートをどう変更するか)は、自分自身のステートと文字だけによって決定されている。文字'0'を見たときのステートマシンの動作を図にすると:
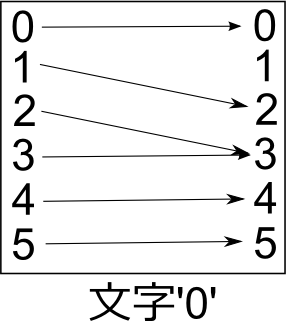
この図は文字'7'についても描ける:
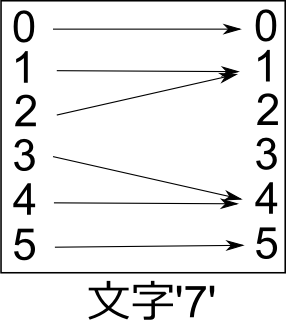
左右に続けて描くと、ステートマシンの逐次的な動作を目で追うことができる:
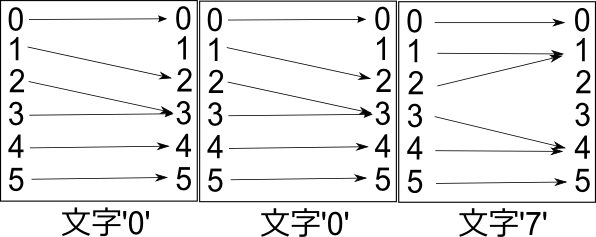
さてここまでは個々の文字についてステートマシンの動作を図に描いてきた。が、上の続けて描いた図を見ると、まったく同じ形式で、文字列についての図が描けることに気付く:
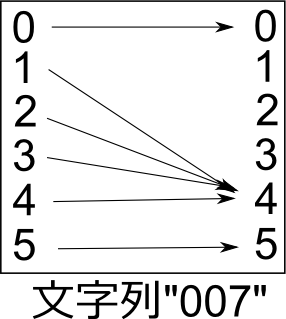
3つの動作を結合して1つの動作にしたわけだ。
この結合は、文字列『007』の例でもわかるとおり、隣り合う動作同士であれば行える。文字列の先頭から逐次的に結合してゆく必要はない。たとえば文字列『abc(』と『)abc』の動作をそれぞれ計算し、それをさらに文字列『007』の動作と続けて描くと:
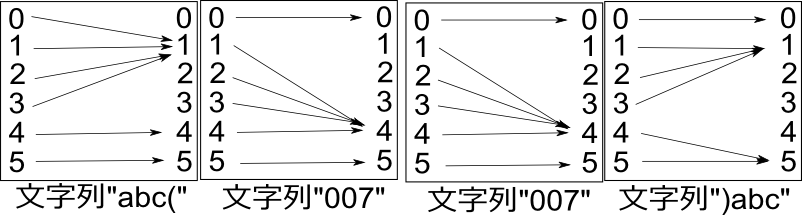
これは文字列『abc(007007)abc』の動作となる。
文字を動作に変換するのがMap、隣り合う動作同士を結合するのがReduceであることは言うまでもない。