2011年01月30日
風洞なしで
平坦な道路における自転車の走行抵抗を、野外で測定することを試みた。
結論:
・風の弱い日(平均1.5m/s)、風向きや風速の変動によるばらつきは50%程度
・2回の測定を密接に連続して行う場合、測定同士の相対的なばらつきは20%程度
ちなみに40km/h時の走行抵抗は300~350Wで、ロープロファイルのホイールとZIPP 808の空気抵抗の差は6W、つまり1.7~2%。
・競技に役立てたければ、風速計とパワーメーターを同時に使うのがいいかもしれない
しかし風速計とパワーメーターの精度からいっても、精度はよくて5%程度だろう。
諸言
自転車ロードレースやトライアスロンにおいて、自転車の走行抵抗は重要な関心事である。平坦な道路での走行抵抗は大半が空気抵抗から生じており、風洞実験を用いた空気抵抗の最小化が有効である。しかし風洞実験の費用はアマチュアには大きな負担である。そこで本研究では、最小限の装置による走行抵抗の測定を試みた。
装置
自転車としてロードバイク(質量10kg)を用い、身長173cm体重60kgの人間が乗った。
自転車の後輪スポークに磁石を、シートステーに磁気センサ(リードスイッチ)を取り付け、後輪が1回転するごとに信号として検出されるようにした。これにデータロガーをつなぎ、信号の検出された時間を記録した。記録の時間解像度は1マイクロセカンドである。
実験
並走する自動車等のない平坦な舗装道路上で、一連の測定を行った。実験時の平均風速は1.5m/s、風向きは道路に平行だった。
自転車を40km/hまで加速させてから12.5km/hに至るまで惰行させ、惰行中の後輪の回転を記録した。この測定を往路3回、復路2回行った。搭乗者は測定中の姿勢をできるかぎり同一かつ一定に保った。
結果
図1に測定結果の一例を示す。横軸は後輪の累積回転数、縦軸は時間(秒)である。
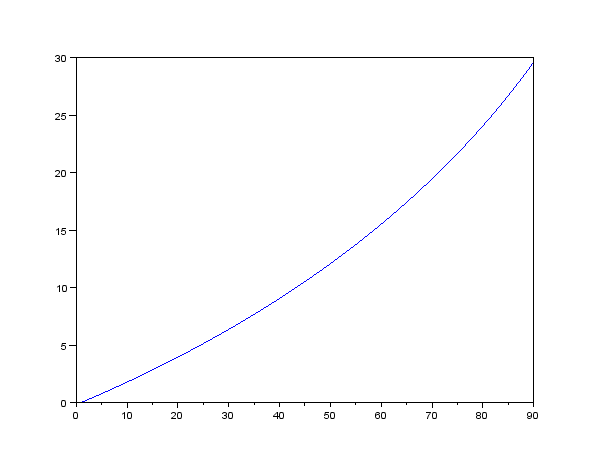
図1 測定結果の一例
考察
平坦な道路を惰行中の自転車は走行抵抗により単調に減速する。走行抵抗が空気抵抗と転がり抵抗からなり、空気抵抗が速度の2乗に比例し、転がり抵抗が速度に依存しないと仮定すると、式1に示す関係が成り立つ。
![]() (式1)
(式1)
ただしF(x)は走行抵抗(N)、aは転がり抵抗(N)、bは空気抵抗係数(N・s2・m-2)、vは対地速度(m/s)、wは対気速度(m/s)とする。また以下ではtは時間(秒)、xは走行距離(m)とする。
式1を数値積分すると関数t=T(x)、v=V(x)が得られる。各測定結果をT(x)にあてはめて非線形最小2乗法でa、b、w、x=0時のvの推定値を得たが、1回の測定を除いてa、b、wは合理的な値とならなかった。
理由は風速の揺らぎと、一見平坦に見える道路のわずかな起伏にあると考えられる。運動エネルギーの20Jの誤差は、a、b、wの推定値を大きく狂わせるのに十分だが、もし道路に3cmの起伏があれば、それ以上の誤差が生じる。測定値とT(x)の差をΔtとし、Δx=Δt・V(x)とすると、Δx・F(x)は運動エネルギーの誤差の推定値を与える。図2.1と2.2の横軸にx、縦軸にΔx・F(x)を示す。
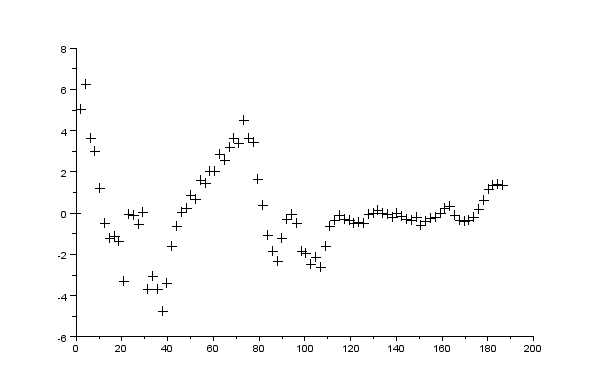
図2.1 合理的な値を得た例 a=3.41, b=0.235, w=1.32 しかしこのaも過大である
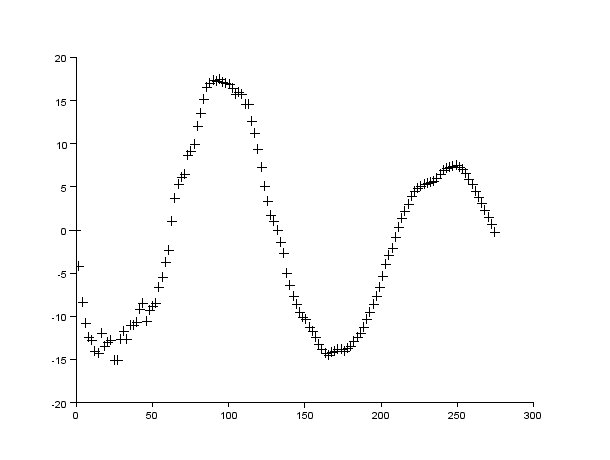
図2.2 合理的な値にならなかった例 a=1.00(制約範囲の下限), b=0.158, w=2.67
そこで、1回の測定の全区間について一組のa、b、wを推定するかわりに、任意の測定点について一組のa、b、wを推定することを試みた。任意の測定点の後に続く10点分の区間を取り出し、この区間についてa、b、wを推定するものである。こうして得られるa、b、wは、それ自身は合理的な値とならないが、bを合理的な範囲に制約すれば、式1により測定点での走行抵抗を推定できる。また、vがV(x)に近い値であれば、合理的な値を得られる。
このようにして得られた走行抵抗を図3.1から3.5に示す。横軸は後輪の累積回転数、縦軸は走行抵抗(ワット)である。
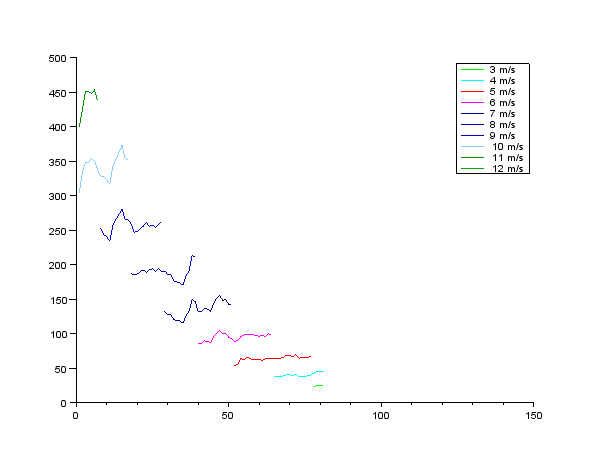
図3.1
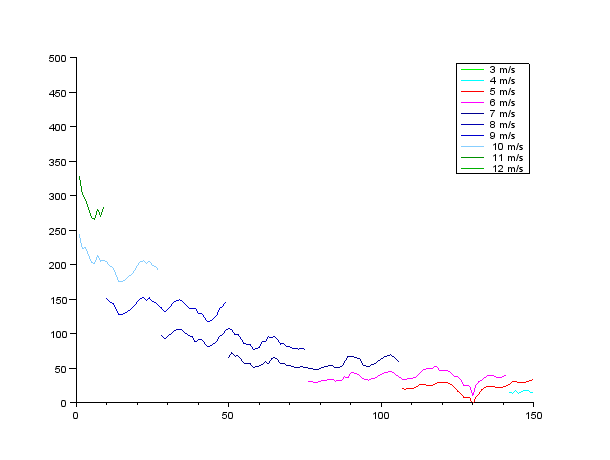
図3.2
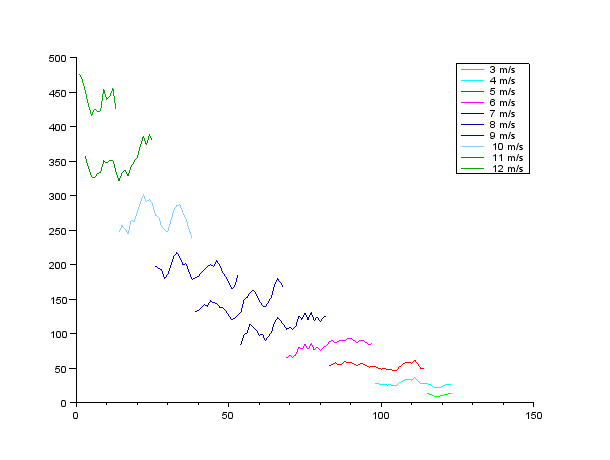
図3.3
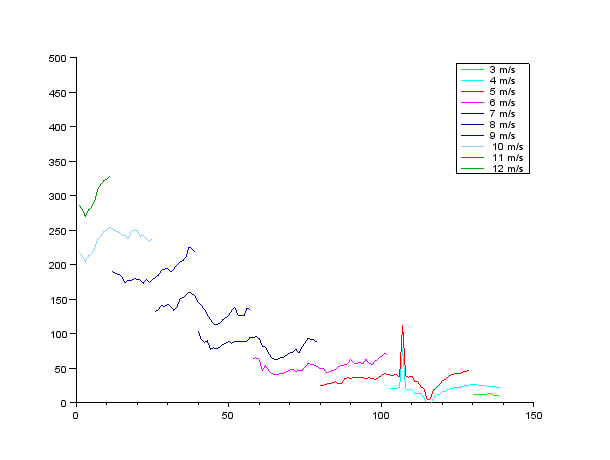
図3.4
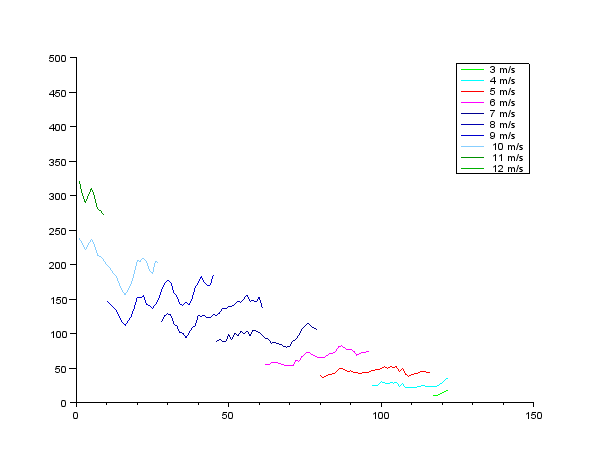
図3.5
図3.1の測定時には強い向かい風だったと考えられる。惰行した距離が短く、走行抵抗も他の測定より高く出ている。惰行した距離と走行抵抗のこのような関係は、全測定結果を通して見られる。時間幅が短いほど風速の変動幅も小さい、という傾向がうかがえる。
空気抵抗を強く反映する10m/s以上の走行抵抗に注目すると、測定間での差は50%程度、1回の測定内での変動は20%程度見られる。この精度では、おおまかな目安を与えることはできるが、競技のために空気抵抗の最小化を図る上ではまったく役に立たない。
結論
本研究の方法では、本研究の目的は達せられないことを示した。
雑感
5%以下の空気抵抗の差は、かなり理想的な条件のもとでも、屋外で検知することは難しい。
風速の揺らぎは空気抵抗に大きな影響を与え、数秒間での変動幅は20%に達する。測定時間を長くし、揺らぎを平均化によって抑え込もうとしても、状況は改善しない。時間幅が長いほど風速の変動幅も大きくなるためだ。2%以下の空気抵抗の差を「体感」したとかいう体験談は、健康食品の効果なるものの「体感」と同様のものである。
逆に、10%以上の差は検知しうる。エアロバーはドロップハンドルに比べて空気抵抗を25%減らせるというが、この差は明らかに感じ取れるだろう。エアロヘルメットやディープリムやスキンスーツは、単体では差を検知できない。しかし3点セットなら差を感じ取れる可能性がある。
現在、本研究の目的を達するうえで有望と思う方法は、パワーメーターと風速計の併用である。レジャー用のハンディ型風速計をハンドルバーに取り付けて、自転車の対気速度を測定し、対気速度を一定に保つようペダリングしながら出力を見る。
対気速度が十分に大きければ(目安としては10m/s以上)、一見平坦に見える道路のわずかな起伏を無視できる。天候(気圧・気温・湿度)による空気の粘性の違いは避けられないが、測定値の賞味期限を1時間程度に設定し、その時間内で最小化の作業を行えばよい。この方法の精度は、賞味期限内での天候の変化、風速の揺らぎ、風速計とパワーメーターの精度に制約されるが、うまくいけば5%程度の精度が得られるのではないかと思う。
(iBikeのiAeroはCdAまで計算してくれるらしいが、風速計のサイズからいって、値段に見合う精度が得られるかどうか疑問に思う。空気抵抗の最小化の作業は始終行うものではないので、あれほど小さな風速計を用いるべき必然性はない。また、本研究を通じて私は、iBikeの開発姿勢に不信の念を抱いた。たとえwが風速計によって与えられても、目に見えない程度のわずかな起伏があればa、bの推定は大きく狂うのに、iBikeのcoast down testはまさにこれをやっている。最近、2 mile rideというキャリブレーション方法が新たに追加されたらしいが、むべなるかなだ)